Previous page     Contents     Next page

The phase transformations between olivine, b-phase (wadsleyite) and spinel (ringwoodite, g -phase) are important for controlling the dynamics of subduction, rheology and the state of stress in subducting slabs and probably for the occurrence of deep-earthquakes. The mechanisms and kinetics of these phase transformations have been investigated mostly under near-hydrostatic stress conditions, which may not be realistic for subduction zones. Although shear stress has been shown to greatly enhance transformation rates, the specific mechanisms involved have not previously been identified.

To study the effect of non-hydrostatic stress on the transformation of b-phase to spinel and the deformation mechanism of b-phase at low temperature, we have carried out high pressure experiments in a multianvil apparatus. A special sample assembly has been designed to impose a non-hydrostatic stress on the sample. Our starting material consisted of San Carlos olivine powder that was hot pressed at 11 GPa and 1250°C for 2h before being deformed. Samples have been deformed either in the b-phase stability field at 15 GPa and 900°C for 30 min or in the (b+g) stability field at 16 GPa and 900°C for 11h. The transformed products and their defect microstructures have been investigated by transmission electron microscopy.

Grains of b-phase in the sample deformed at 15 GPa have low densities of dislocations (< 3.10¹² m^-2) and variable densities of stacking faults parallel to (010). These stacking faults extend right across individual grains. The density of stacking faults does not reach a maximum in grains with (010) planes at 45° of the principal compressive stress, i.e. the orientation of maximum shear stress. This indicates that stacking faults were not formed during deformation by the glide of glissile partial dislocations. The second sample deformed at 16 GPa is composed of b-phase grains with a higher dislocation density (< 10¹³ m^-2). Some dislocations form well-organized pure-tilt subgrain boundaries parallel to (100) while free b=[100] dislocations are curved, showing that climb is active in b -phase at 900°C. Because climb is diffusion controlled and does not occur in olivine at 900°C, it appears that diffusion is faster in b-phase than in olivine at 900°C. These grains contain very few stacking faults, also running from one grain boundary to the other, suggesting that stacking faults are growth defects that anneal out with time. This sample also contains numerous small (300 nm diameter) disk-shaped inclusions of g -phase which show a topotaxial relation to the host b -phase: (100)_b // (110)_g ; (010)_b // (110)_{g ;} (001)_b // (001)_g. These inclusions have nucleated at the intersection of (010) stacking faults and dislocations with b=[100] (Fig 3.1-3 and 3.1-4).
 

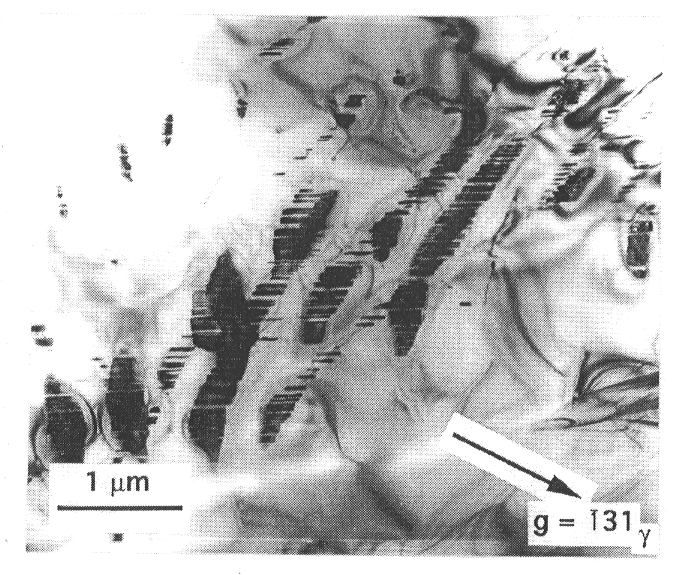Fig 3.1-3: Bright field image of disk-shaped inclusions of g-phase (dark) in a host b-phase grain. The maximum length (diameter) of the inclusions lies parallel to (010).

Because differential stress controls the density of dislocations, the rate of intracrystalline nucleation of g in b must be stress-dependent. Stress would thus enhance the kinetics of the b-g transformation. Analytical TEM of the b-phase host and the spinel inclusions shows that spinel is significantly enriched in Fe₂SiO₄ compared to b-phase. Therefore growth of spinel may be diffusion-controlled. The dislocations that connect the spinel inclusions may enhance growth by providing a rapid diffusion pathway (pipe diffusion). The enhanced nucleation and growth provided by deformation-induced dislocations suggests that differential stress in subducting slabs plays an important role in b-g transformation kinetics.

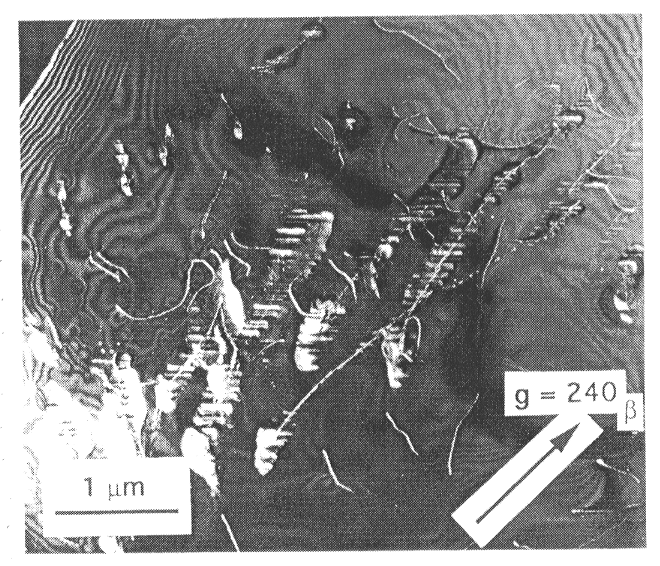Fig 3.1-4: Weak beam image of b= [100] dislocations in the same area as in the previous micrograph. Inclusions have nucleated along these dislocations.