Previous page     Contents     Next page

Members of the apatite family of minerals are not only subsidiaries in almost all igneous rocks but are also found in sedimentary and metamorphic rocks. They are the most abundant of phosphorus-bearing minerals with a general formula Ca₅(PO)₄(OH,F,Cl) where fluorine, chlorine and the hydroxyl ion can be mutually substituted to form pure end-members. Apart from being an extremely important accessory in a large number of mineral systems, apatite is a 'reservoir' of rare earth, or large-lithophile elements which are commonly used as petrological tracers. These tracers in themselves do not constitute any major mineralogical phase, nor are that accommodated in the major phases due to their low abundances and large ionic radii, but they are of vital importance for determining the chemical constitution of the mantle through geochemical and tectonic processes.

Although apatite controls the Earth's budget of both phosphorus and light rare earth elements, and contains significant quantities of the volatile halide elements, relatively little is known about its compressional behaviour. To form accurate thermodynamic models of apatite in the Earth's deep interior, and to hence establish a better understanding of the behaviour of the large lithophile tracer elements and phosphorus, it is crucial that the equation-of-state is determined accurately. Towards this end we have performed high-pressure powder-diffraction experiments on the three end-member materials Ca₅(PO₄)₃F, Ca₅(PO₄)₃OH and Ca₅(PO₄)₃Cl using angle-dispersive techniques and an image plate area detector on ID9 (BL3) at the European Synchrotron Radiation Facility (ESRF). A wavelength of 0.4735 Å was selected from the multipole wiggler radiation using both a mirror and a monochromator and the samples were pressurised in BGI and DXR5 diamond anvil cells with a 4:1 methanol-ethanol mixture as a pressure transmitting medium. A typical example of the high quality of data obtained can be seen in Fig. 3.3-13 which shows a full structure Rietveld refinement of Ca₅(PO₄)₃OH powder data collected at 9.8 GPa.

The unit cell volumes for the three end-members are plotted as a function of pressure to 10 GPa in Fig. 3.3-14. The solid lines are Birch-Murnaghan fits to the data, with the constraint
 

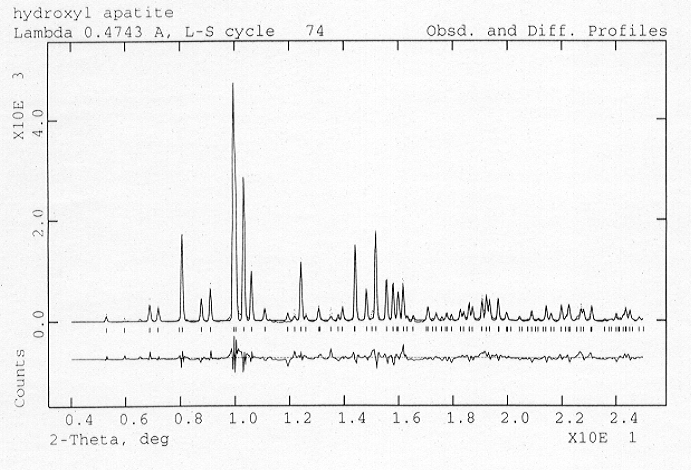Fig. 3.3-13: One-dimensional X-ray diffraction profile obtained by reduction of image-plate data obtained from Ca5(PO4)3OH held at 9.8 GPa in a diamond-anvil cell. Dots are the experimental data and the solid line is the result of a full-pattern Rietveld refinement of the structure. The quality of the fit is indicated by the small magnitude of the difference between the two (bottom trace).

K' = 4 in all cases, which give K₀ = 97.5(1.8) GPa, 97.9(1.9) GPa, and 93(4) GPa for Ca₅(PO₄)₃F and Ca₅(PO₄)₃OH and Ca₅(PO₄)₃Cl respectively. Data were also collected to 20 GPa for Ca₅(PO₄)₃F and Ca₅(PO₄)₃OH and to 50 GPa for Ca₅(PO₄)₃Cl but, as the samples were no longer under hydrostatic conditions due to freezing of the methanol-ethanol pressure media, the data were not used for the equation-of-state determination. The data above 10 GPa indicated, however, that there is no strong evidence for a structural phase transition in any of the end-members and it can be expected that the apatite structure is stable, at least with respect to pressure, within the lithosphere.
 

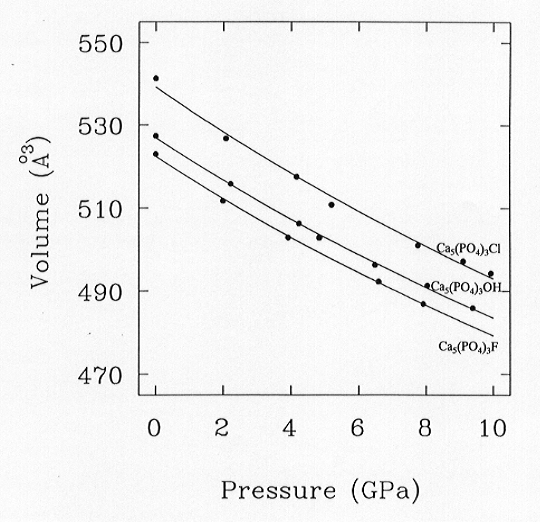Fig. 3.3-14:  Volume variation of the three apatite phases with pressure, together with the equations of state fitted to the data. All three apatite members show very similar compression behaviour.