

During the collapse of a lava dome or during decompression of cryptodomes
by landslides the average decompression rate can be estimated as ˜
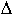 P/
P/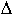 tdec
, where
tdec
, where 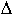 tdec is the characteristic
time for the pressure drop,
tdec is the characteristic
time for the pressure drop, 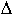 P. The
fundamental criterion as to whether the magma can respond in a fully viscous
manner is the timescale of deformation implicit in the application of the
differential or volume stress at the potential fragmentation interval.
The Maxwell relation relates the viscosity of the melt phase,
P. The
fundamental criterion as to whether the magma can respond in a fully viscous
manner is the timescale of deformation implicit in the application of the
differential or volume stress at the potential fragmentation interval.
The Maxwell relation relates the viscosity of the melt phase, 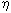 ,
to its (structural and stress) relaxation timescale,
,
to its (structural and stress) relaxation timescale, 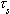 ,
as
,
as 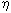 /M=
/M=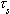 , where M is the elastic modulus. The relation can be expressed
for either the volume or the shear component of stress, or for their combination,
the longitudinal stress. To a good approximation the Maxwell model of a
simple linearly viscoelastic material can also predict the onset of non-Newtonian
response of the melt phase to an applied stress. Experimental determinations
of the onset of non-Newtonian viscosity can be normalised using the Maxwell
relaxation time to show that, regardless of composition, the onset of non-Newtonian
behaviour occurs at 3 log units of deformation timescale above (or log
units of deformation rate below) the Maxwell prediction.
, where M is the elastic modulus. The relation can be expressed
for either the volume or the shear component of stress, or for their combination,
the longitudinal stress. To a good approximation the Maxwell model of a
simple linearly viscoelastic material can also predict the onset of non-Newtonian
response of the melt phase to an applied stress. Experimental determinations
of the onset of non-Newtonian viscosity can be normalised using the Maxwell
relaxation time to show that, regardless of composition, the onset of non-Newtonian
behaviour occurs at 3 log units of deformation timescale above (or log
units of deformation rate below) the Maxwell prediction.
Prediction of the critical strain rate necessary for the onset of non-Newtonian rheology, and with it the prediction of the critical timescale of deformation to generate an elastic accumulation of stress in the magma, ultimately enabling brittle failure, is thus a question of determining the viscosity and elastic modulus (shear, volume or longitudinal) of the melt in question. The viscosity is converted into a timescale via the Maxwell relation from which a log factor of 3.0 must be subtracted to account for the non-Newtonian onset that has been observed experimentally. For example a water-poor (0.1 wt%) calcalkaline rhyolite at low pressure (several tens of bars) and 900°C has been estimated to have a volume viscosity of 108.5 Pa s. This corresponds to a relaxation time, via the Maxwell relation, of 10-1.5 s (using a bulk modulus of 10 GPa). The non-Newtonian onset is estimated to occur at a timescale 3.0 log units removed, or 101.5 s, corresponding to a deformation rate of 10-1.5 s. Analysis of the behaviour of viscous magma under short-term tensile stresses demonstrates that the volume strain rates anticipated in the eruptive stages of silicic volcanic systems may be high enough under certain circumstances to generate runaway non-Newtonian shear thinning plus subsequent fragmentation of the melt by brittle failure.
Among the material properties and intensive parameters which should influence magma fragmentation during rapid decompression are 1) the physical state of the magma (e.g., vesicula-rity + vesicle contents, vesicle pressure, crystallinity), 2) the rheological (e.g. viscosity, yield strength) and mechanical (e.g. tensile strength, elastic moduli) properties. Relevant intensive parameters must include the initial pressure (or pressure differential), the temperature and the decompression rate. These parameters can best be estimated from a combination of observations of explosive eruptions and laboratory studies of the products of such eruptions.
Two simplified physical models of the state of vesicular magma undergoing rapid decompression have been considered. In the first model magma has only isolated vesicles. In the second model all vesicles are connected. In the latter case vesicular magma can be considered as permeable. The analysis of the behaviour of such simplified model materials undergoing one-dimensional tension should help to understand mechanisms of highly viscous vesicular magma fragmentation.
Three mechanisms for the fragmentation of highly viscous magma by rapid decompression have been considered and evaluated. These are 1) fragmentation by the propagation of a pressure release wave, 2) fragmentation by the propagation of a fragmentation wave and 3) fragmentation by rapid filtration flow. These mechanisms have been compared for the cases of magmas (a) containing closed, isolated pores (vesicles) and (b) containing open, connected pores. The analysis shows that release wave fragmentation mechanism can work for both types of highly-viscous magma (isolated vesicles/connected vesicles). The fragmentation wave mechanism requires predominantly closed vesicles, and the rapid filtration flow mechanism requires connected vesicles.
Different physical scenarios for the decompression of magma have been compared in terms of the likelihood of fragmentation by the above mechanisms. It has been concluded that the detailed nature and efficiency of the primary fragmentation event and the pyroclastic products of such an event can be expected to vary widely depending on the dominant mechanism. Thus the most effective fragmentation (finest fragments) should occur when mechanisms of fragmentation by release wave and fragmentation wave work together.

Tel: +49-(0) 921 55 3700 / 3766, Fax: +49-(0) 921 55 3769, E-mail: bayerisches.geoinstitut(at)uni-bayreuth.de
 Previous page
Previous page