

The determination of accurate and precise cell parameters and unit-cell volumes of crystalline materials at high pressures opens up a number of areas of research, including the precise determination of equations of state (EOS´s), the evaluation of critical strain behaviour at structural phase transitions under high pressures and the more precise measurement of pressure itself. The measurement of pressure is one of the major contributions to uncertainties in high-pressure experiments. For single-crystal diffraction at high pressures in diamond-anvil pressure cells (DACs) the common solution is to use the ruby fluorescence technique to determine pressure. This has the advantage that the ruby crystal used for these measurements need only be a few microns in size and thus it occupies a very small proportion of the limited sample volume in a diamond-anvil cell and it contributes very little diffracted intensity. However, although the pressure-induced wavelength shift of the ruby fluorescence spectrum can be readily measured to a precision equivalent to approximately 0.01 GPa or better in pressure, the residual data scatter in plots of crystal volumes determined by diffraction against pressures determined from the ruby fluorescence shift is significantly greater than the estimated errors. The reasons for this appear to be related to temperature variations: most ruby fluorescence measurements are, by necessity, made away from the four-circle diffractometer and temperature changes can contribute to apparent pressure differences due to the strong temperature dependence of the ruby spectrum (a 5-6°C temperature change gives the same shift as a 0.1 GPa pressure change) and to real pressure changes because of the differential thermal expansion of the components of the DAC.
These sources of uncertainty are readily overcome by the use of an internal diffraction standard to determine pressure in the DAC. The requirements for such a standard are that it should be a high symmetry, low-unit-cell volume crystal to minimise the interference with the diffraction pattern from the sample, it must be chemically stable in both air and the pressure edia used in the DAC, and it must have a well-known equation of state with which to convert measured unit-cell volumes to pressures. Other considerations are that the material is readily prepared in small crystals with small mosaic spread due to the presence of subgrains to maximise signal-to-noise in the diffraction pattern and to produce sharp peaks whose positions can be measured precisely on the diffractometer. Fluorite meets these criteria, and has frequently been used as an internal pressure standard, but it's use is restricted to pressures of less than 9.2 GPa because at this pressure it undergoes a phase transition that destroys single crystals.
A second standard material is therefore required to allow precise measurements of pressure in excess of 9.2 GPa. In addition, the choice of a softer material than fluorite would result in increased precision in pressure for the same precision in unit-cell volume measurement. Both of these requirements would be met by the use of NaCl which remains in the B1 phase to 30 GPa, and whose room pressure bulk modulus is 25 GPa compared to the 81 GPa of fluorite. Use of NaCl would therefore, in principle, provide a factor of 3 improvement of precision in pressure measurement. But, although NaCl is widely used as an internal pressure calibrant in powder-diffraction experiments performed at high pressures, problems with it dissolving in popular pressure media such as alcohol and the difficulty of obtaining single crystals with small mosaic spread preclude its general use for single-crystal diffraction measurements. Therefore we have chosen quartz as an internal pressure calibrant because it has none of the problems associated with NaCl, meets the requirements noted above and has a lower bulk modulus (K~37 GPa) than fluorite. In addition, the trigonal symmetry of quartz allows an internal cross-check from the unit-cell parameters a and c for the presence of anisotropic strains and its low shear strength means that even small non-hydrostatic pressure conditions lead to very large increases in the mosaic spread and hence the widths of diffraction peaks. We have therefore undertaken a cross-calibration study of quartz with fluorite to determine its EOS more precisely.
Single-crystal diffraction measurements were performed with the Huber four-circle goniometer installed at the Bayerisches Geoinstitut which was described in the Annual Report of last year. Single crystals of quartz and fluorite were loaded simultaneously in a diamond anvil pressure cell of our own design (also described in the 1995 Annual Report) with methanol: ethanol as pressure medium. Unit cell parameters of both crystals were determined from the positions of the diffracted beams at 22 pressures to a maximum pressure of 8.9 GPa (limited by the transformation in fluorite). Room-pressure unit-cell determinations performed on several different crystals of fluorite and quartz (held in the DAC without pressure fluid) over a time period of approximately 9 months yield a population standard deviation of both unit-cell edges and unit-cell volumes that is less than the mean of the esd's of the individual measurements. This indicates not only the stability and reproducibility of the diffractometer configuration, but also that the esd's in cell parameters obtained from the vector least squares of the data are a reasonable estimate of the true precision of the measurements.
The pressure of each experiment was derived from the measured unit-cell
volume of the fluorite crystal through the previously determined EOS of
fluorite with parameters Vo=163.063(7)Å3, KTO =
81.0 GPa and K' = 5.22. The precision in individual unit-cell volume determinations
for fluorite range from 1 part in 8,500 to 1 part in 20,000, with a mean
of 1 part in 12,500. Because of the increase in magnitude of dP/dV with
increasing pressure, the resulting precision in pressure measurement from
fluorite also varies with the pressure. The mean precision in unit-cell
volume corresponds to a precision of about 0.008 GPa at 1 GPa to 0.011
GPa at 9 GPa. The unit-cell parameters and volume of quartz are slightly
inferior, with precision in volume ranging from 1 part in 5,000 to 1 part
in 16,000 with average of 1 part in 9,000. Equation of state parameters
of quartz were determined by a least-squares fit of a third order Birch-Murnaghan
EOS to the volume data with pressures determined from the fluorite from
which we obtain V0 = 112.981(2) Å3, KTO
= 37.12(9) GPa and K' = 5.99(4), with 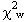 = 0.95. This EOS has a maximum residual |Pobs-Pcalc | of 0.025 GPa (Fig.
3.8-1).
= 0.95. This EOS has a maximum residual |Pobs-Pcalc | of 0.025 GPa (Fig.
3.8-1).
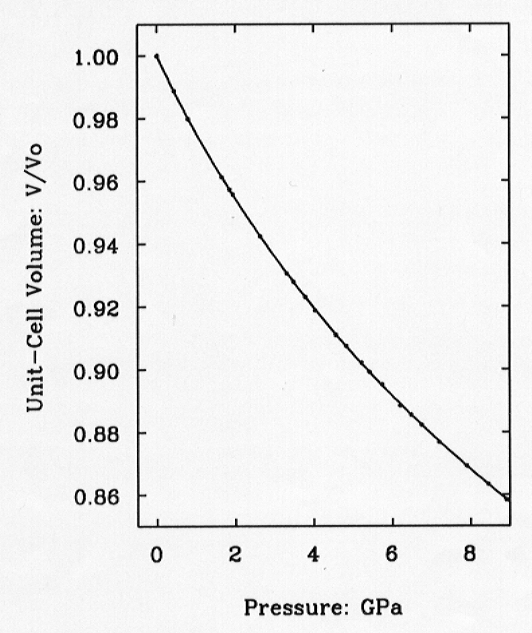 |
Fig. 3.8-1: Variation of the unit-cell volume of quartz with pressure as determined by single-crystal diffraction. Symbol sizes exceed experimental uncertainties. The line is the fitted equation of state. |
The closeness of the value of 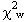 to unity indicates that the esd's in unit-cell volumes derived from the
least-squares fit to the diffractometer angles represent a realistic estimate
of the true precision of the experimental technique. The accuracy of the
equation of state that we have measured for quartz can be assessed through
a comparison with independent determinations of the elastic constants of
quartz at high pressure. These latter yield KTO = 37.12(6) GPa
in perfect agreement with our value, and K' = 6.3(3), which is also in
agreement with our determination within the uncertainty of the ultrasonic
measurement.
to unity indicates that the esd's in unit-cell volumes derived from the
least-squares fit to the diffractometer angles represent a realistic estimate
of the true precision of the experimental technique. The accuracy of the
equation of state that we have measured for quartz can be assessed through
a comparison with independent determinations of the elastic constants of
quartz at high pressure. These latter yield KTO = 37.12(6) GPa
in perfect agreement with our value, and K' = 6.3(3), which is also in
agreement with our determination within the uncertainty of the ultrasonic
measurement.
The new equation of state for quartz provides a precise internal pressure standard for single-crystal high-pressure diffraction experiments. If the unit-cell volumes of quartz can be determined to a precision of 0.0001 (1 part in 10,000) then the resulting precisions in pressure will be 0.004 GPa at 1.0 GPa, 0.006 GPa at 5 GPa and 0.009 GPa at 9 GPa (=0.1%), compared to precisions from fluorite of 0.009, 0.010 and 0.013 respectively. Because the value of K' of quartz is larger than that of fluorite, the relative advantage of quartz as an internal pressure standard over fluorite decreases with increasing pressure by a factor of approximately two over this pressure range. The other factor to consider in the choice between the use of quartz and fluorite is the actual precision with which the unit-cell volumes can be measured. For the same volume of crystal the signal level from quartz is lower than that from fluorite, leading to a lower precision in the final unit-cell volumes. Our average precisions in volume for the two materials (1 part in 12,500 for fluorite, 1 part in 9,000 for quartz) yield much closer precisions in pressure, with quartz being marginally better for pressure determination at lower pressures and marginally worse than fluorite at 9 GPa. Thus quartz is more suited to pressure measurement at low pressures and, of course, can be used at pressures in excess of the limit of 9.2 GPa at which fluorite undergoes a phase transition which is destructive of single crystals.

Tel: +49-(0) 921 55 3700 / 3766, Fax: +49-(0) 921 55 3769, E-mail: bayerisches.geoinstitut(at)uni-bayreuth.de
 Previous page
Previous page