

The viscosity of silicate melts is a powerful constraint on the nature and efficiency of magmatic processes. As early as the 1930s Bowen pointed out that one of the most important physical distinctions between basaltic and rhyolitic volcanism lies in the extraordinary difference in viscosities between the two systems at their eruptive temperatures. Silicic magmas are often inferred to have been H2O-rich during their petrogenesis and the influence of H2O on the viscosity of silicic melts has a long history of investigation which has concentrated in more recent years on the effects of relatively high H2O contents on the viscosity of rhyolitic and granitic melts. Very recently, however, attention has turned again to the region of relatively low H2O contents and relatively high viscosities. This is due in part to increasing interest in the physics of eruptive processes and the potentially dominant role of viscosity in controlling the processes involved in melt degassing and fragmentation.
Despite the fact that models for the calculation of melt viscosity have been around for 25 years, prediction of the viscosity of hydrous granitic melts is complicated by the fact that the temperature dependence of the viscosity is significantly non-Arrhenian. Here we present an empirical model to account for the non-Arrhenian temperature dependence.
For the purposes of our fit we have extracted all the available viscosity data for hydrous metaluminous leucogranitic melts, some 111 data points, from the literature. These data were used as input in the fitting, neglecting the influence of pressure dependence and the speciation of the dissolved H2O on the viscosity of hydrous granitic melts.
For our approach we have rewritten the Vogel-Fulcher-Tammann (VFT) equation so that the VFT-parameters are replaced by expressions, a, b and c, introducing a composition dependence (H2O concentration) of each VFT-parameter:
log 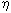 = a (wt% H2O) + b
(wt% H2O) / [T - c (wt% H2O)] (1)
= a (wt% H2O) + b
(wt% H2O) / [T - c (wt% H2O)] (1)
We have fitted the viscosity data to different functional forms using a standard nonlinear regression technique. Of the solutions, equation (2) yielded the best fit statistics for the calculation of melt viscosities of metaluminous leucogranitic melts under crustal pressures with a standard deviation of 0.46 log10 units:
log  = (-3.545 + 0.833 ln(w)) + (9601 -
2368 ln(w)) / [T - (195.7 + 32.25 ln(w))] (2)
= (-3.545 + 0.833 ln(w)) + (9601 -
2368 ln(w)) / [T - (195.7 + 32.25 ln(w))] (2)
where  is the viscosity in Pa s, w is H2O
concentration in wt%, and T is in K.
is the viscosity in Pa s, w is H2O
concentration in wt%, and T is in K.
The non-Arrhenian temperature dependence incorporated in equation 2 contrasts with all preceding methods (Baker (1996), American Mineralogist, 81, 126-134; Scaillet, Holtz, Pichavant, Schmidt (1996), Journal of Geophysical Research 101(B12), 27691-27699; Schulze, Behrens, Holtz, Roux, Johannes (1996), American Mineralogist 81, 1155-1165; Shaw (1972) American Journal of Science 272, 870-889) for the calculation of hydrous granitic melt viscosities that have been based exclusively on Arrhenian relationships. The comparison of those methods with the present one (Fig. 3.7-1) clearly indicates the significant improvement in the quality of fit obtained from incorporating the very important non-Arrhenian temperature dependence of hydrous melt viscosities.
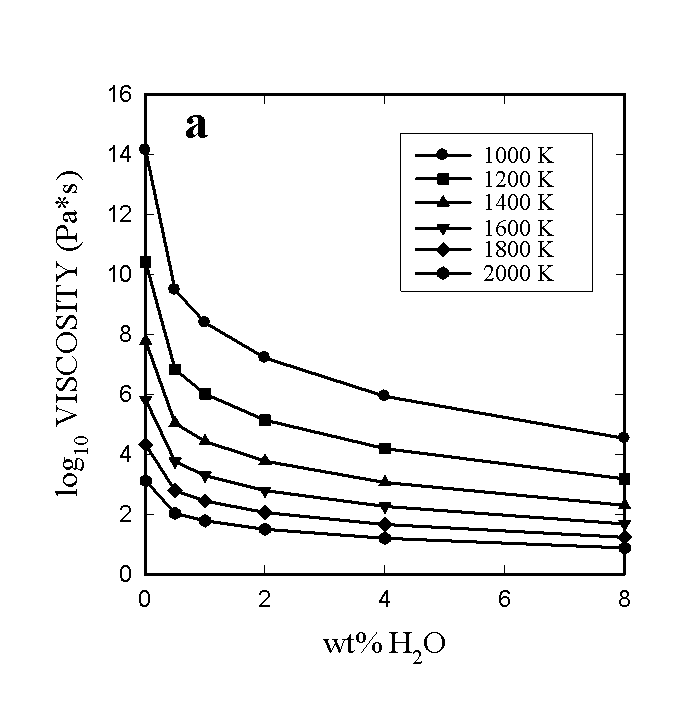
All of the essential features of the temperature- and composition-dependence
of the viscosity of hydrous metaluminous granitic melts appear to be well
reproduced by the new model. Figure 3.7-2 illustrates the predicted isothermal
variations of viscosity with H2O content (fig. 3.7-2a) as well
as the variation of viscosity with temperature at constant H2O
content (Fig. 3.7-2b). Some aspects of these calculations worth noting
here are (1) the model is capable of predicting viscosities over the entire
H2O content range from 0 to 12.5 wt% within the 0.46 log10
unit accuracy. The particularly sensitive region of very low H2O
contents is well-described and no apparent crossover of viscosity curves
at high temperatures and low H2O contents exists, at least up
to 2500K. (2) The degree of nonlinearity of the decrease in viscosity with
H2O content is a strong function of the temperature. At lower
temperatures, very extreme decreases in viscosity are caused by the addition
of a few tenths of a wt% of H2O. (3) Slight variations in the
compositions of the various granitic, haplogranitic and rhyolitic melts
used as input can be neglected for the purpose of hydrous melt viscosity
calculation. On the basis of the success of this parameterization, the
neglect of pressure and speciation effects would appear to be justified.
We recommend its use for all petrologic
 |
Fig. 3.7-1: Comparison of various viscosity models with our new model. |
 |
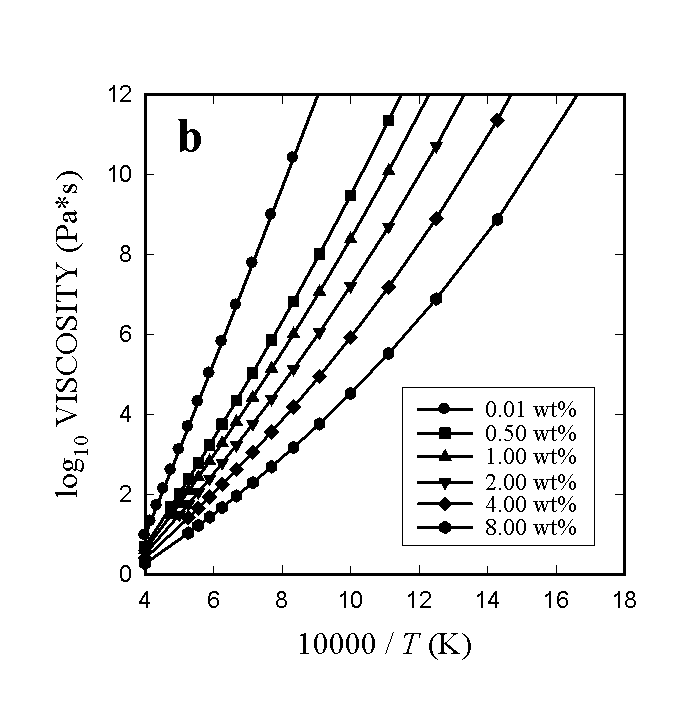 |
Fig. 3.7-2: The viscosity of a hydrous leucogranitic melt as a function of a) water content for different temperatures and b) temperature for different water contents. Note the highly non-linear increase of viscosity at low temperatures and low water contents in Fig. 3.7-2a. |
|
calculations involving hydrous, metaluminous, leucogranitic melts. It is an especially powerful improvement at the high viscosities thought to be relevant to erupting silicic volcanic systems and magmatic hydrothermal granitic and pegmatitic systems at the brittleductile transition.

Tel: +49-(0) 921 55 3700 / 3766, Fax: +49-(0) 921 55 3769, E-mail: bayerisches.geoinstitut(at)uni-bayreuth.de
 Previous page
Previous page